In a previous article you learned about How NRCS Hydrographs Are Made. This article takes the discussion to a deeper level and explains the effect the Unit Hydrograph has on the final runoff hydrograph. It also describes how you can easily modify the Unit Hydrograph’s Shape Factor (a.k.a. Peaking Factor) to match your local drainage ordinance, if it requires a modified Unit Hydrograph.
For example, the states of Michigan, Florida and Delaware and nearby regions (Delmarva), each employ non-standard Unit Hydrograph Shape Factors. These can be easily be replicated in Hydrology Studio without having to use other software, spreadsheets, etc., with just a single data entry in the Project Settings… the Shape Factor.
What’s a Unit Hydrograph?
A unit hydrograph is essentially a hydrograph that is derived from an excess of 1 inch of rainfall on a watershed within a specific time period, such as 1 minute. It does not represent the ultimate runoff hydrograph, but rather showcases the distinctive attributes of the watershed. Consider the unit hydrograph as comparable to an individual’s DNA. Once the unit hydrograph for a specific watershed is determined, any design storm can be utilized to calculate the final runoff hydrograph.
If all unit hydrographs (UH) conform to a constant shape, that is, a constant amount of volume under its rising limb, then both the time and discharge ordinates can be normalized to produce a dimensionless UH. The flows can be expressed as ratios of the UH peak Q and the timeline values can be measured as ratios of the time-to-peak (Tp). So once we know the peak Q of this unit hydrograph, we can display it with some real numbers.

The peak discharge for the Unit Hydrograph is computed as:

Where:
Qp = peak outflow, cfs (cms)
484 = Shape Factor (Peaking Factor) (0.208 metric)
A = catchment area, sq. miles (sq kilometers)
Q = total excess precipitation, 1 inch (1 mm)
Tp = time to peak (hrs)
The Time to Peak, Tp, and the Time Base, Tb, are what determines the characteristics of the Unit Hydrograph. These values are computed as follows:
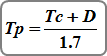
Where:
Tp = time to peak (hrs)
Tc = time of concentration (hrs)
D = time interval (hrs)
Where Did 484 Shape Factor Originate?
The NRCS, formerly known as the SCS, analyzed numerous real watersheds across the country and formulated a standardized dimensionless UH with 37.5% of the volume falling under the ascending limb. Upon establishing an equation to calculate Qp in cfs, Tp in hours, A in square miles, and Q in inches, a constant was necessary to manage all these conversions… 484.
It was also discovered that the turning point on the downward slope occurred at around 1.7 times Tp, serving as the foundation for the form of the initial curvilinear unit hydrograph. A demonstration of the corresponding triangular UH can be observed below in a real watershed.

It’s Not a “One Size Fits All”
Throughout the years, the utilization of the 484-based SCS dimensionless hydrograph has consistently resulted in overestimations of discharges in flat, swampy terrains. Conversely, in mountainous regions, it tends to underestimate discharges. This discrepancy in estimation can vary from 23 to 45 percent compared to the standard UH-484 edition. Depending on the specific location and topography of a project, adjustments to the standard UH might be necessary.
One way to achieve this is by modifying the Shape Factor. Decreasing the Shape Factor in areas where overestimations occur and increasing it in regions where underestimations are prevalent can help align the peak discharge values. The Shape Factor essentially adjusts the UH while ensuring that the total volume under the hydrograph remains consistent at 1 inch.
Here’s an example: In the state of Michigan a study was done to evaluate whether the shape of the standard NRCS Dimensionless UH is applicable to Michigan streams.
Turns out it wasn’t.
The study analyzed 24 gaged streams and 74 different flood events. The results demonstrate that the recorded floods are best reproduced if the UH has just 28.5 percent of its volume under the rising limb instead of the standard 37.5.
In an effort to provide guidance to the engineering community, they devised a set of UH ordinates that produce a UH that fits their 28.5 rising limb rule, and aptly named it the MDEQ SCS Method. These ordinates are 0.0, 0.5, 1.0, 0.8, 0.6, 0.4, 0.2 and 0; and Tc <= 60 minutes. Unless you’re intimately familiar with how unit hydrographs are constructed, you may be inclined to plug those ordinates into WinTR-something and let it produce the hydrographs.
The good news is that Hydrology Studio generates its unit hydrographs on the fly. There’s no need to specify ordinates of a custom unit hydrograph.
The good news is that Hydrology Studio generates its unit hydrographs on the fly. There’s no need to specify ordinates of a custom UH. Just enter the appropriate Shape Factor in the program’s Settings and you’re good to go.
You can easily determine the Shape Factor by dividing the desired percentage rising limb volume by the standard UH of 37.5 and multiplying by 484. So in Michigan’s case, 28.5/37.5 x 484 = 368.
Below is the MDEQ SCS Method UH for a typical drainage area produced by Hydrology Studio by simply using a Shape Factor of 368.

The chart confirms the Peak Factor of 368 precisely re-shapes the Michigan UH so that only 28.5 percent of the volume is under the rising limb, and the remaining volume on the descending side. It also proves the UH adheres to the MDEQ ordinates while maintaining the required total volume from 1-inch of precipitation.
Below is an overlay of the Standard and the MDEQ SCS unit hydrographs for a 10-acre drainage area. It should be noted that while one can modify the Peak Factor, the volume under the UH must remain at 1-inch over the drainage area. Hydrology Studio maintains this volume for you.

Below are final runoff hydrographs of the same drainage area using a 6-hour design storm, overlaid. Notice they both peak at the same time but have different peak discharges and volumes.

Use this same procedure for any other unit hydrograph recipe. For example, the Delmarva Unit Hydrograph, DUH, requires 22 percent of its volume under the rising limb. The Peak Factor can be computed using the ratio of (22/37.5) x 484 = 284.
One More Thing…
It is common to come across information regarding drainage authorities mandating the utilization of distinct Shape Factors for runoff modeling before and after development. Research conducted by the New Jersey Department of Agriculture (NJDA) suggests that the level of urbanization plays a minor role in the flow distribution and, consequently, the Shape Factor.
The findings of the NJDA study align with those of NRCS, which advises against altering unit hydrographs when estimating runoff before and after development. NRCS sensitivity studies indicate that no single characteristic of a watershed has a significant correlation with the Shape Factor of the unit hydrograph (peak rate).
Bottom line… avoid mixing and matching Shape Factors in the same pre- and post-development project.
