The Rational method was developed over 100 years ago and continues to be used for urban watershed modeling, typically on areas less than about 20 acres. While there exists many varieties of the Rational method, Stormwater Studio uses the most popular… the Standard Rational.
Standard Rational
The Standard Rational method computes the peak discharge as determined by the well-known Rational formula.
Where:
Qp = peak discharge, cfs (cms)
k = 1 English (0.00278 Metric)
C = runoff coefficient
A = basin area, acres (hectares)
i = intensity, in/hr (mm/hr)
Cf = frequency correction factor where C x Cf <= 1.0
The rainfall intensity is computed by one of the following equations:
FHA Equation
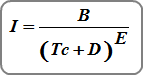
Where:
B, D and E are constants
Tc = time of concentration in minutes subject to the Minimum Tc
Third Degree Polynomial Equation
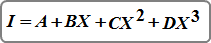
Where:
I = rainfall intensity in in/hr (mm/hr)
X = Ln(time duration in minutes)
A = coefficient
B = coefficient
C = coefficient
D = coefficient
Appropriate values for X are 8 to 180 minutes subject to the Minimum Tc.
The B,D and E constants can be pre-computed by the program, or as manually entered, and are based on your geographic location. Polynomial coefficients can be directly entered in to software as well.
Calculation Procedure for Time of Concentration, Tc
The time of concentration is the time required for water to flow from the remotest point of the drainage area to the point of the system in question. The program computes Tc at each inlet or junction by choosing the greatest of the following:
- The time of concentration of the upstream Line plus the time of flow through the Line from the upstream run.
- The time of concentration as above for any other connecting Line(s).
- The Inlet Time of the Line under consideration.
For the most upstream run, the time of concentration is the Inlet Time. For all succeeding lines, the time of concentration is computed as the largest value of the three items above.
When computing flows for downstream lines, Stormwater Studio uses a total CxA, that is, CA for the Line in question plus CA for the next upstream Line plus CA for the next upstream Line and so on. This insures that all drainage areas are contributing to flow to the catchment of interest.
Rational Method Anomalies
As described above, the flow path having the longest time of concentration to the point of interest in your storm sewer system typically defines the storm duration used in selecting the intensity value in the Rational method. There are some important exceptions that you should be aware of.
You might notice this exception when viewing your Standard Report and the System Tc is extremely long. This is typical of a long narrow wooded lot with a small runoff coefficient that will remain undeveloped but whose flows must cross or be included in the new development. When this rogue area is included in the runoff computation, the resulting long time of concentration will produce smaller Peak Qs and thus pipes designed too small to handle the internal flows from a shorter duration storm. To remedy this, adjustments will need to be made by simply disregarding those rogue areas (or a portion of them) where flow time is too slow to add to the peak discharge.
Here’s what to do and how to do it:
There are generally two scenarios:
1. A highly impervious section exists at the most downstream area of an inlet’s watershed and the rogue upstream area flows through the lower impervious area. Two separate calculations should be made to find the area – either the Total or the Impervious – which produces the highest Q.
• First, calculate the Peak Q from the total drainage area with its weighted C value and the intensity associated with the longest time of concentration, Tc. (Stormwater Studio has probably already done this for you during its normal calculation routine.)
• Secondly, calculate the Peak Q using only the smaller, Impervious Area, its C value and intensity associated with its shorter Tc. (Pull from the IDF curves.)
Compare the two and only use the drainage area, C and Tc that produces the highest Peak Q. This typically will be the smaller area. Disregard the larger, slower area.
2. A smaller, less pervious, area is tributary to the larger primary drainage area. When this scenario occurs, two sets of calculations should also be made.
• First, calculate the Peak Q from the total drainage area with its weighted C value and the intensity associated with the longest time of concentration, Tc. (Stormwater Studio has probably already done this for you during its normal calculation routine.)
• Secondly, prorate the larger drainage area. We need to learn how much discharge from the larger, slower area is contributing at the same time the peak from the smaller less pervious tributary area is occurring. For example, if the smaller tributary area has a Tc of 10 minutes, how much area from the larger, slower area, is contributing after 10 minutes?
Prorate it. We’ll call that prorated area, Ap. It’s the most downstream fractional part of the larger area that will contribute to the flow during the time of concentration associated with the smaller, less pervious area.
Ap = A (Tc1 / Tc2)
Where:
Ap = Prorated area
A = Area of the larger primary area
Tc1 = Time of concentration of the smaller tributary area
Tc2 = Time of concentration associated with the larger area
The C value to be used in this computation should be the weighted C value that results from combining C values of the smaller less pervious tributary area and the prorated area Ap. The area to be used would be the area of the smaller impervious area plus Ap. Your composite Area, C inputs would look similar to the inputs shown below. You would use the shorter Time of Concentration, Tc1.
Please keep in mind that this prorated method assumes a linear relationship between Tc and Area, i.e., the overland travel time is basically constant as it travels downstream.
Tc by TR55
In addition to manual entry, Stormwater Studio can compute Time of Concentration using TR55. With TR55, Tc is broken into 3-components or segments. The final Tc is the sum total of the three components.
- Sheet Flow
- Shallow Concentrated Flow
- Channel Flow
Tc = TSheet + TShallow + TChannel
Sheet Flow Time
Flow over plane surfaces and typically ranges between 125 to 150 feet (40 to 45 meters).
Where:
n = Manning’s roughness coefficient
L = Flow Length (must be <= 100 ft (30 m) per WinTR55)
P2 = Two-year 24-hr rainfall, inches (mm)
S = Land Slope, ft/ft (m/m) – Entered as % in the program
Shallow Concentrated Flow Time
After about 100 feet, sheet flow becomes shallow concentrated flow. The computed Average Velocity described below is based on the solution of Manning’s equation with different assumptions for n (Manning’s roughness coefficient) and r (hydraulic radius, ft). Per TR55, for for paved areas, n is 0.025 and r is 0.2; unpaved areas, n is 0.05 and r is 0.4.
Where:
L = Flow Length, ft (m)
V = Average velocity, ft/s (m/s) and
Where:
Cp = 20.3282 paved surfaces
Cp = 16.1345 unpaved surfaces
S = Watercourse slope, ft/ft (m/m)
Channel Flow Time
Occurs within channels, swales, ditches, streams or even piped systems. Manning’s equation is used to compute velocity.
Where:
L = Flow length, ft (m)
V = Average velocity, ft/s (m/s) and
Where:
V = Average velocity, ft/s (m/s)
R = Hydraulic radius, ft (m) = a/wp
S = Channel slope, ft/ft (m/m) – Entered as % in the program
n = Manning’s roughness coefficient