Outlet control flow conditions are calculated based on energy balance. The total energy required to pass the flow through the culvert barrel is the sum of the entrance loss (He), the friction losses through the barrel (Hf), and the exit loss (Ho).
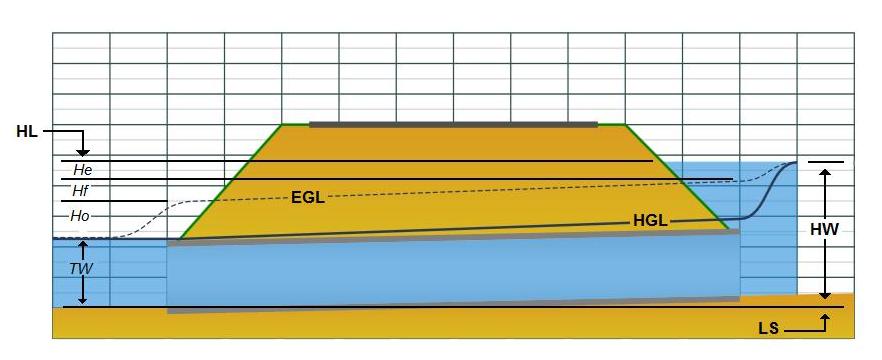
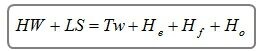
Exit Loss
The exit loss is computed by the following equation:
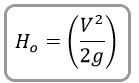
Where:
V = Velocity exiting the culvert
g = Acceleration due to gravity
Friction Loss
Channel Studio uses the energy-based Standard Step method when computing the friction loss. This methodology is an iterative procedure that applies Bernoulli’s energy equation between the downstream and upstream ends of the culvert. It uses Manning’s equation to determine head losses due to pipe friction.
This method makes no assumptions as to the depth of flow and is only accepted when the energy equation has balanced.
The following equation is used for all flow conditions:
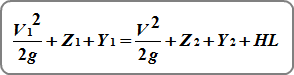
Where:
V = Velocity
Z = Invert elevation
Y = HGL minus the invert elevation
Friction losses are computed by averaging the friction head as follows:

Where:
HL = Energy head loss due to friction
hf1 = Friction head at the downstream end
hf2 = Friction head at the upstream end
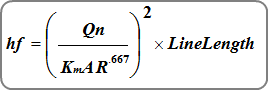
Where:
Km = 1.486 (1.0)
n = Manning’s n
A = Cross-sectional area of flow
R = Hydraulic radius
Composite n-values
Channel Studio uses the Horton-Einstein equation to compute a composite n-value for open-bottom arch sections.
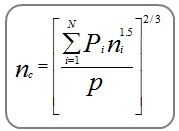
Where:
nc = Composite n-value
Pi = Wetted perimeter of subdivision i
ni = n-value for subdivision i
P = Total wetted perimeter
Entrance Loss
The entrance loss is a function of the velocity head in the barrel, and is expressed as a coefficient times the velocity head.
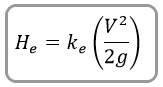
Where:
V = Velocity exiting the culvert
g = Acceleration due to gravity
Ke = Coefficient based on various inlet configurations provided in HDS-5
