Studio Express uses a standard weir equation for Rectangular Sharp-crested, Compound, Cipolletti, Trapezoidal and Rectangular Broad-crested weirs.
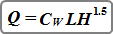
Where:
Q = discharge over weir, cfs (cms)
L = length of the weir crest, ft (m)
H = distance between water surface and the crest, ft (m)
Cw = weir coefficient, typically 3.33 (1.84) for sharp-crested; 3.367 (1.83) for Cipolletti; 3.09 (1.7) for Broad-crested
Trapezoidal with Sloped Sides
Total flow over trapezoidal weirs with side slopes is computed using the standard weir equation as shown above, plus two times the flow given from the following equation.
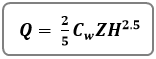
Where:
Q = discharge over side-sloped portion of weir, cfs (cms)
Z = side slope (Z horizontal to 1 vertical) of the weir crest
H = distance between water surface and the crest, ft (m)
Cw = weir coefficient, typically 3.367 (1.83)
V-notch
V-notch weirs are computed using this equation:
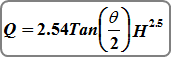
Where: Q = discharge over weir, cfs (cms)
Θ = angle of v-notch in degrees
H = head on apex of v-notch, ft (m)
Adjustment for Submerged Weirs
Weirs can be affected by submergence, i.e., when the user-inputted tailwater rises above the weir’s crest.
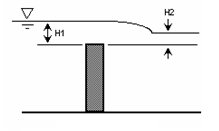The equation for the reduction in flow is:
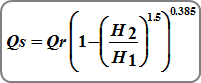
Where:
Qs = submerged flow, cfs (cms)
Qr = unsubmerged flow from standard weir equations, cfs (cms)
H1 = upstream head above crest, ft (m)
H2 = downstream head above crest, ft (m)
New to our site? Learn more about Hydrology Studio’s complete suite of stormwater design software.
- Hydrology Studio
- Stormwater Studio
- Culvert Studio
- Channel Studio
- Studio Express